Hyperparameters: The Heart of Machine Learning Model Optimization
Next — Today I Learnt About Data Science | Issue #81
My internship project at HP requires us to experiment several models in limited time. My work is to forecast demand of all print products in all geographies. HP is a big company; they manufacture over 18,000 products and sell it in over 170 countries. How would you know how much to produce of each kind and to transport where?
There are at least two ways to create such demand forecasts.
First, we get several inputs from our customers — Walmart, Staples, Amazon — on their expected demand. They have their own customer analytics team which predicts the demand for different printers. Additionally, many corporate buyers like universities and companies put their demands in advance — sometimes even up to six months in advance. Different corporate deals progress at different rates and we have some estimates on expected demand from every channel. Operations research has built hundreds of models of this kind.
Secondly, we have estimates on product demands using analytical methods. Time-series forecasting, historically, has only considered time-series models like ARIMA.
In the last several years, many new models have come to limelight including Machine Learning decision tree-based learners like LightGBM, Random Forest, Meta’s Prophet, and more. My project was focussed on these ML models.
Almost all of these models require optimization of different hyperparameters.
What are hyperparameters?
Creating predictive models requires data; that’s obvious. With that data, the model estimates several parameters that are used to estimate the ground truth model as closely as possible. However, some design choices are necessary.
For example, at what point should a parameter move to a new parameter value? How much should it move by? How many attempts should it make for every group of parameters?
These meta-decisions are controlled using hyperparameters. These need to be determined before training the model itself. This places us in a Catch-22 situation. You cannot know the if a set of hyperparameters are good before training the model, and you cannot train the model without choosing a set of hyperparameters.
How to choose hyperparameters?
Consider for a moment, you are an Oracle. You know what are the best hyperparameters. This implies you can train your algorithm with your data and get the best model. In my case, at HP, it took around eight hours to train every model with a given set of hyperparameters.
Now, bring yourself back to reality. You are not an Oracle. You do not know the best hyperparameters. But you still need to find the best model-.
Hogwarts has several possibilities for our Harry. Here are the big three.
Let’s understand each of them in little more detail.
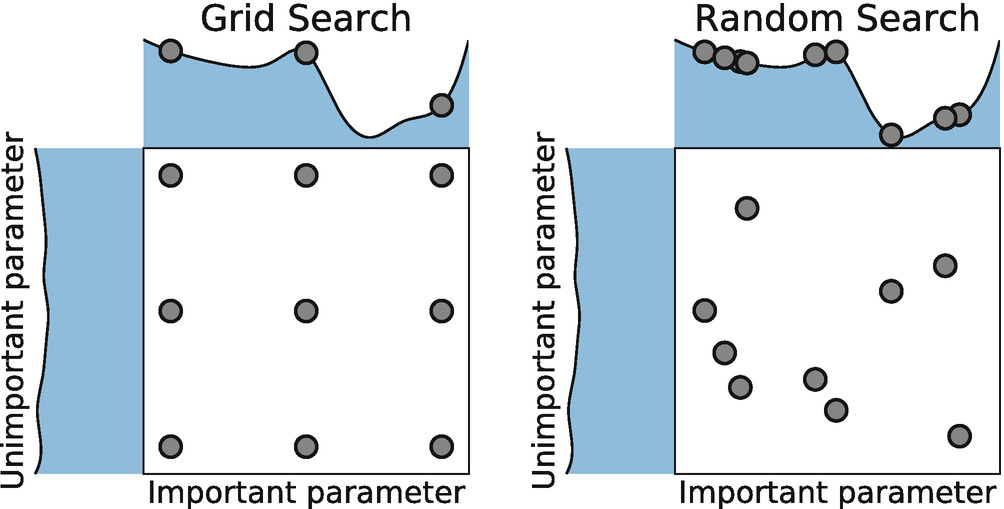
Grid Search
This method involves defining a subset of the hyperparameter space as a grid of hyperparameter values and then systematically working through all combinations. Though this approach can be computationally expensive, it's thorough as it considers every single possible combination in the grid.
Random Search
As the name suggests, this method involves randomly selecting the hyperparameters from the complete grid to use for each iteration of the training model. This approach can be more efficient than grid-search as it doesn’t waste time on all combinations. However, it also might miss the optimal combination.
Bayesian Search
This is a more advanced method that involves creating a probabilistic model of the function mapping from hyperparameters to the loss associated with the model. This technique is usually more efficient than both random and grid search as it uses past evaluation results to choose the next values to evaluate. Optuna, which I will cover next week, implements it for general use.
LightGBM Hyperparameters
To give you an example of how this all works, I will use the example from LightGBM — the model I’ve played extensively with in the last two years,
Here is a brief list of hyperparameters in LightGBM and how they affect the complete model. (Official documentation)
Number of Leaves: This is the main parameter to control the complexity of the tree model. Theoretically, we can have num_leaves = 2^(max_depth) to obtain the same number of leaves as depth-wise tree. However, this is not a good strategy because the tree nodes grow exponentially with the increase in depth, causing overfitting.
Minimum Data In Leaf: This is a very important parameter to prevent over-fitting in a leaf-wise tree. Its optimal value depends on the number of training samples and num_leaves. Setting it to a large value can avoid growing too complex a tree, but may cause under-fitting.
Max depth: It describes the maximum depth of tree. This parameter is used to handle model overfitting. Any time you feel the model is overfitted, lower max_depth.
Bagging fraction: Specifies the fraction of data to be used for each iteration and is generally used to speed up the training and avoid overfitting.
Feature fraction: Specifies the fraction of features to be used for each iteration. Like bagging fraction, this is also used to handle overfitting.
Learning Rate: This determines the impact of each tree on the final outcome. GBM works by starting with an initial estimate which is updated using the output of each tree. The learning parameter controls the magnitude of this change in the estimates. Lower values are generally preferred as they make the model robust to the specific characteristics of the tree and thus allowing it to generalize well.
Example of Grid Search and Random Search
Let's assume you have your training data in variables X_train and y_train.
Grid Search
Let's consider we are tuning only two hyperparameters for LightGBM: 'max_depth' and 'num_leaves'. We can define a set of possible values for 'max_depth' as [5, 10, 15] and 'num_leaves' as [20, 30, 40]. Grid-search will then train the LightGBM model for all combinations of 'max_depth' and 'num_leaves' — that's 9 combinations! For each of these combinations, the model's performance will be evaluated, for instance, using cross-validation. Finally, the set of hyperparameters that yielded the model with the best performance is chosen.
See sklearn’s documentation for details.
from sklearn.model_selection import GridSearchCV
import lightgbm as lgb
# Define the grid of hyperparameters to search
hyperparameter_grid = {
'max_depth': [5, 10, 15],
'num_leaves': [20, 30, 40],
}
# Create a LightGBM model
lgbm = lgb.LGBMRegressor()
# Set up the grid search with 3-fold cross validation
grid = GridSearchCV(lgbm, hyperparameter_grid, cv=3, n_jobs=-1)
grid.fit(X_train, y_train)
# Get the optimal parameters
best_params = grid.best_params_Random Search
Continuing with the LightGBM example, we can specify the range of 'max_depth' to be from 5 to 15 and 'num_leaves' to be from 20 to 40. Instead of trying out all 9 combinations like in grid-search, random search might only try out a specified number of combinations, say 5, chosen randomly from within the specified range.
These combinations could be, for instance, ['max_depth' = 10, 'num_leaves' = 30], ['max_depth' = 5, 'num_leaves' = 20], ['max_depth' = 15, 'num_leaves' = 40], ['max_depth' = 7, 'num_leaves' = 35], ['max_depth' = 11, 'num_leaves' = 25]. The performance of the model is evaluated for each of these combinations, and the one that gives the best model is chosen.
See RandomizedSearchCV for details.
from sklearn.model_selection import RandomizedSearchCV
import lightgbm as lgb
# Define the grid of hyperparameters to search
hyperparameter_grid = {
'max_depth': [5, 10, 15],
'num_leaves': [20, 30, 40],
}
# Create a LightGBM model
lgbm = lgb.LGBMRegressor()
# Set up the random search with 3-fold cross validation
randomCV = RandomizedSearchCV(lgbm, hyperparameter_grid, cv=3, n_jobs=-1, n_iter=5)
randomCV.fit(X_train, y_train)
# Get the optimal parameters
best_params = randomCV.best_params_Note that n_jobs=-1 will use all available cores on your machine. n_iter is the number of parameter settings that are sampled in random search. In the case of grid search, all possible combinations are evaluated, but for random search, you can control the number of combinations to be tested.
What’s Next
Choosing hyperparameters is indeed an art that requires a balance between performance and computational efficiency. It is also important to keep in mind that a combination of hyperparameters that works well for one dataset might not work as well for a different one. Hence, hyperparameter tuning is usually done in the context of cross-validation to ensure that the chosen values work well for unseen data.
In the next part of this series, we will discuss Optuna, a Python library for optimizing machine learning hyperparameters, to make this process less daunting and more streamlined. Stay tuned!
Unrelated Readings
I hope you enjoyed today’s deep dive into hyperparameters. Let me know whether you liked it or not!
— Harsh